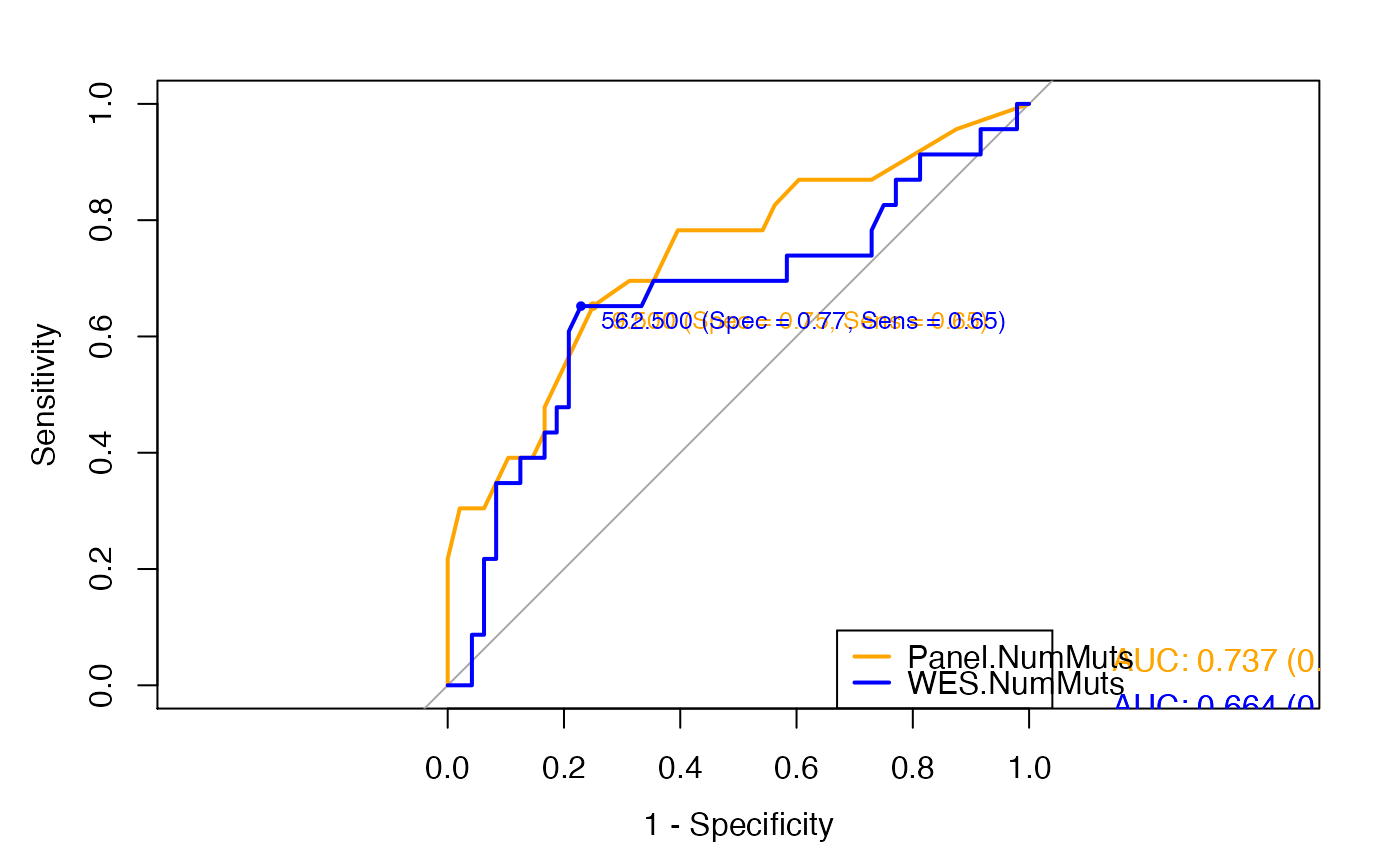
Generate and compare two ROC curves of TMB performance in immunotherapy responder classification

This function takes in input two sets of TMB values for the same samples and a binary variable representing the clinical response to immunotherapy. It generates two ROC curves showing performance of the two TMB datasets to discriminate between responders and nonresponders, as well as the best TMB cutoff.

compareROC(dataset, TMB1, TMB2, method, paired, boot.n)

Arguments

dataset	a data.frame containing numeric vectors of TMB values and a factor with name 'ClinicalResponse' and levels 'responder' and 'nonresponder'
TMB1	character string indicating the data.frame column containing TMB values from the first approach
TMB2	character string indicating the data.frame column containing TMB values from the second approach
method	character string indicating the method to use: delong, bootstrap or venkatraman. See roc.test for more details.
paired	a logical indicating whether you want a paired roc.test. If NULL, the paired status will be auto-detected by are.paired. If TRUE but the paired status cannot be assessed by are.paired will produce an error. See roc.test for more details.
boot.n	for method="bootstrap" and method="venkatraman" only: the number of bootstrap replicates or permutations. Default: 2000. See roc.test for more details.

Value

Returns in standard output the result of the test used to compare the two ROC curves and a pdf file containg plots of the ROC curves and their respective AUC, sensitivity and specificity values and the best threshold for sample classification.

See also

roc.test

Author

Laura Fancello

Examples

## Compare the ROC curves representing the performance of panel-based and
## WES-based TMB to predict clinical response with the default delong method.

# Set the seed to create reproducible train and test sets in generateROC
set.seed(949)


# Read TMB values and response to immunotherapy
data(Hellman_SimulatedFM1Panel_WES)

# Compare ROCs
compareROC(dataset = Hellman_SimulatedFM1Panel_WES,
           TMB1 = "Panel.NumMuts",
           TMB2 = "WES.NumMuts",
           method = "d",
           paired = TRUE)
#> Setting levels: control = nonresponder, case = responder
#> Setting direction: controls < cases
#> Setting levels: control = nonresponder, case = responder
#> Setting direction: controls < cases
#> 
#> 	DeLong's test for two correlated ROC curves
#> 
#> data:  TMB1 and TMB2 by as.factor(dataset$ClinicalResponse) (nonresponder, responder)
#> Z = 1.05, p-value = 0.2937
#> alternative hypothesis: true difference in AUC is not equal to 0
#> sample estimates:
#> AUC of roc1 AUC of roc2 
#>   0.7368659   0.6644022 
#> 
#> Setting direction: controls < cases
#> Setting direction: controls < cases